حادث عابر… يُنتج نظريات رياضية !

د. أبو بكر خالد سعد الله
قسم الرياضيات، المدرسة العليا للأساتذة (الجزائر)

         قُبيل نهاية عهدة الرئيس الأمريكي جورج بوش الأب (1924-2018)، كانت سفينة بضائع قد أقلعت من مدينة هونغ كونغ الصينية متّجهة نحو الولايات المتحدة الأمريكية. وكان على متنها عدد من الحاويات، منها حاوية مُلِئت بألعاب مائية للصغار ليتسلّوا بها في أحواض المياه أو في المسابح المنزلية. وهذه الألعاب الملوّنة المصنوعة في الصين هي بطّ أصفر وقنادس حمراء وضفادع خضراء وسلاحف زرقاء. وكانت السفينة سترسو في ميناء مدينة تاكوما Tacoma الواقعة جنوب مدينة سياتل Seattle في ولاية واشنطن.

غير أنه عندما وصلت السفينة يوم 10 يناير 1992 إلى شمال المحيط الهادي واجهتها ليلا عاصفة هوجاء في مكان ليس ببعيد عن الموقع الذي غرقت فيه سفينة تايتنك الشهيرة، أدّت إلى سقوط 12 حاوية في مياه المحيط، منها الحاوية التي تحمل 29 ألف لعبة من تلك الألعاب المائية. وقد انفتحت حاوية الألعاب في مياه المحيط، وربما كان سبب الانفتاح الاصطدام العنيف لهذه الحاوية بالسفينة ذاتها أو بالحاويات أثناء تساقطها. ومن المهمّ في هذا الموضوع أن نعرف أن كل لعبة من الألعاب صُنعت من المطاط القوي الذي لا ينفذ منه الماء. وقد وُضعت في كيس من البلاستيك داخل علبة من الورق المقوى.

أظهرت الاختبارات اللاحقة أن الورق المقوى تحلّل بسرعة كبيرة في مياه المحيط، مما سمح للألعاب بالتخلّص من العلب الورقية، ثم إن الغلاف البلاستيكي يتآكل ولا يؤثر في حركة تلك الألعاب على سطح المحيط. وهكذا، تحرّرت نهائيا من كل القيود، وراحت تسبح في الماء لأنها ليست مثقّبة ولا تمتص الماء خلافا لكثير من الألعاب المائية الأخرى.

تنبّؤ كورتيس إبيسمير

ولد عالم المحيطات الأمريكي كورتيس إبيسمير Curtis Ebbesmeyer عام 1943. وقد درس، بعد تقاعده، حركة الحطام العائم في المحيطات. ولفت الأنظار كثيرا عند اهتمامه بشحنة هذه الألعاب المطاطية بعد انتشارها في المحيط الهادي عام 1992.

وقبل ذلك، اهتم إبيسمير بتيارات المحيط متتبّعا العوامات والبضائع التي تسقط من السفن التجارية في المحيط الهادي. ففي شهر مايو 1990، تساقطت شحنة أحذية رياضية تُقدَّر بثمانين ألف حذاء من العلامة العالمية (نايك) في مياه المحيط الهادي، وراحت تطفو على سطح ماء المحيط في مناطق التيارات القوية. حاول إبيسمير آنذاك رصد حركتها لتعقّب تيارات المحيط على سواحل ولايتي أوريغون Oregon وواشنطن الأمريكيتين المطلّتين على المحيط الهادي. كما اهتم بتتبّع 34 ألف قُفازة خاصة بلعبة الهوكي كانت قد انتشرت في مياه المحيط عام 1994. وانشغل قبل ذلك بموضوع انسكابات وتسرّبات النفط ومياه الصرف الصحي والتنبؤ بمساراتها. ومن المعلوم أن إبيسمير أسّس عام 1996 الرابطة الدولية لعلماء المحيطات.

 وهكذا، قام إبيسمير بالتعاون مع مساعده جيمس إنغراهام James Ingraham بنمذجة حركة التيارات على سطح المحيط الهادي، وذلك في سياق أبحاثه المرتبطة بتتبّع حركة ومسار الألعاب المطاطية المشار إليها آنفا. ذلك أن وجود عدد هائل من تلك الألعاب دفعة واحدة على سطح المحيط يوفّر للباحثين امتيازات في دراسة الظاهرة لا توفّرها الطرق التقليدية التي تعتمد على نشر زجاجات انجراف بعدد قليل (لا يتجاوز ألف زجاجة في التجربة الواحدة)، مقارنة بعدد هذه الألعاب الذي يقارب 30 ألف لعبة. فمن بين تلك الامتيازات أن علماء المحيط لا يسترجعون في تجاربهم سوى نسبة ضئيلة من الزجاجات (لا تتجاوز 20 زجاجة في كل تجربة)، في حين أنهم قدّروا إمكانية استرجاع نحو 600 لعبة من تلك الألعاب التائهة في المحيط. وهذا ما يسمح لهم بالتعمّق في أبحاثهم الخاصة من خلال تتبّع مسارات حركة تيارات المحيط الهادي. لذا كانت هذه الألعاب فرصة من ذهب للباحثيْن إبيسمير وإنغراهام.

قطعت تلك الألعاب بين 1992 و2007 مسافة تناهز 28 ألف كيلومتر، حيث طافت فوق الموقع الذي غرقت فيه سفينة تايتنك، ونزلت حتى بلغت شواطئ جزر هاواي، بل إنها قضت سنوات مجمّدة داخل كيس جليدي في القطب الشمالي. وخلال عام 2007 اتجهت تلك الألعاب مباشرة إلى السواحل البريطانية كما توقّع إبيسمير، ملاحظًا أنه سيكون من السهل على روّاد الشواطئ البريطانية اكتشاف الألعاب لأنها فقدت ألوانها عندما تساقطت في مياه المحيط قبل 15 سنة وتحوّلت إلى اللون الأبيض!

لقد أصاب إبيسمير حين تنبّأ بما اعتقد الكثيرون باستحالته؛ فقد تنبأ بأن الآلاف من هذه الألعاب سينتهي بها المطاف في جليد القطب الشمالي بالقرب من ألاسكا، ثم ستتحرك بسرعة 1.6 كيلومتر/اليوم، وهي متجمدة داخل كتل جليدية نحو المحيط الأطلسي! وقد ثبتت صحة هذا التنبؤ بعد سنوات. ففي عام 2003، عُثر على أولى هذه الألعاب على الساحل الشرقي للولايات المتحدة وكندا.

وبهذه الحركة ساعدت الألعاب الباحثين على رسم خارطة كبرى تيارات المحيطات لأنه عندما يتم رصدها وهي تتمايل على الأمواج، فمن المرجح أن يسارع الناس إلى إبلاغ السلطات عنها أكثر مما يفعلونه عند ملاحظتهم العوامات التقليدية التي يستخدمها العلماء. إنها ألعاب لا تقدّر بثمن بالنسبة لعلماء المحيطات حتى إن الشركة الأمريكية التي وجهت إليها هذه البضاعة صارت تقدم مكافأة لمن يعثر على إحدى هذه الألعاب.

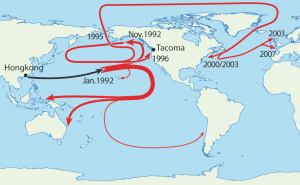
 أبرز محطّات رحلة الألعاب

– 10 يناير 1992: وقوع الحادث وسط المحيط الهادي.

– 16 نوفمبر 1992: على بعد نحو 3200 كيلومتر من مكان الحادث، عثر أحد عمال الشواطئ بالقرب من مدينة سيتكا Sitka  على 10 ألعاب في منطقة  الدوامات شبه القطبية (Subpolar Gyre).

– 28 نوفمبر 1992 / أغسطس 1993: بعد أن اتصل كورتيس إبيسمير وجيمس إنغراهام بعمال الشواطئ وسكان السواحل من أجل تعقّب الألعاب التي تقطعت بها السبل على طول نحو 850 كم من السواحل، اكتشفت 20 لعبة يوم 28 نوفمبر 1992. وتمّ حتى أغسطس 1993 العثور على ما مجموعه 400 لعبة على طول الساحل الشرقي لخليج ألاسكا.

– مطلع عام 1995: استغرقت الألعاب ثلاث سنوات في الدوران، من موقع الحادث إلى ألاسكا، ثم غربًا وجنوبًا إلى اليابان، قبل العودة شمالًا وشرقًا، مروراً بموقع الحادث الأصلي، ثم النزول مرة أخرى إلى أمريكا الشمالية؛ مع العلم أنه عثر على بعضها في جزر هاواي. وكانت الإدارة القومية الأمريكية للمحيطات والغلاف الجوي (NOAA) قد تأكدت من أن سرعة هذه الألعاب تفوق سرعة مياه التيار بنسبة 50%.

– 1995 / 2000: استطاعت بعض الألعاب مغادرة منطقة الدوامات شبه القطبية والتوجّه نحو الشمال عبر مضيق بيرينغ  Bering. وتجمّدت الألعاب عند اقترابها من القطب الشمالي، وتحركت باستمرار باتجاه الشرق.

– 2000: بدأت تلك الألعاب تصل إلى شمال المحيط الأطلسي، وحينها بدأ الجليد بالذوبان وتواصل التحرك نحو الجنوب. وهكذا، سرعان ما شوهدت الألعاب تتمايل فوق أمواج المحيط الأطلسي من ولاية مين إلى ولاية ماساتشوستس الأمريكيتين.

– النصف الثاني من عام 2003: قدمت الشركة الأمريكية التي وجهت إليها البضاعة مكافأة قدرها 100 دولار لمن يعثر على هذه الألعاب في نيو إنغلاند أو كندا أو أيسلندا.

– 2004: جُمع الكثير من الألعاب مقارنة بما جُمع خلال عام 2003. ومع ذلك، كانت الكمية المحصل عليها أقل مما كان متوقعا.

– يوليو 2007: عثر شخص على بطة بلاستيكية على ساحل ديفون Devon الواقع جنوب غربي إنكلترا، واعتقد صحفيون بريطانيون أن الأمر يتعلق بلعبة من ألعاب حادث 1992، وراحوا يعلنون عن وصول تلك الألعاب إلى شواطئ ديفون. لكن الباحث سيمون بوكسل Simon Boxall، من المركز القومي البريطاني لعلوم المحيطات في ساوثهامبتون فحص البطة وأكد أنها ليست من ألعاب 1992.

المنطق الرياضي وقابلية البتّ

         دعنا نربط هذا الموضوع المتشعّب بمفهوم رياضي يُدعى “قابلية البتّ” Undecidability. من أجل ذلك نحتاج إلى بعض التمهيدات: فمن منطلقات منطق الرياضيات الحديثة أن الصواب لا يأتي منه إلا الصواب، في حين أن الخطأ ينجم عنه الخطأ والصواب على السواء. أما “القضية” في المنطق الرياضي فتدلّ على جملة لا نستطيع الحكم عليها إلا بأحد الأمرين: إما أنها صحيحة أو أنها خاطئة، مستبعدين بذلك أي احتمال ثالث (وفق “مبدأ الثالث المرفوع” المبني عليه المنطق الرياضي المعروف في المدارس والجامعات).

         لقد أدت الأبحاث في الرياضيات خلال القرن العشرين إلى وضعية غريبة: هناك قضايا غير قابلة للبتّ، أي إننا لا نستطيع البتّ في صحتها أو في خطئها ببرهان رياضي سليم. وبالأحرى، إذا انطلقت من فرضية صحتها تمكنت من البرهان على أنها خاطئة. كما أن انطلاقك من فرضية خطئها يمكّنك من إثبات صحتها!

من كان وراء هذا المفهوم الغريب؟ إذا صنّفت كبار علماء الرياضيات خلال القرن العشرين حسب عدد مؤلفاتهم فستجد أن أولهم على الإطلاق (في الزمن والمكان) هو المجري بول إردوش Paul Erdos (1913-1996) الذي بلغ إنتاجه 1552 بحثا، منها 465 بحثا أنجزها منفردا، والبقية نشرها بمعية مئات الباحثين الآخرين عبر العالم. وستكتشف أن آخر هؤلاء العلماء -من حيث عدد البحوث المنشورة- هو النمساوي، أبو المنطق الرياضي الحديث، كورت غودل Kurt Godel (1906-1978) الذي لم يتجاوز عدد بحوثه 60 بحثا على الرغم من وقعها العميق على رياضيات القرن العشرين وتوجهاتها.

كان عالم الرياضيات الألماني ديفد هيلبرت Hilbert David (1862-1943) يعتقد أننا نستطيع اعتبار الرياضيات جملة من العمليات الشكلية (الصورية) والمنطقية لرموز تستند إلى مسلّمات وضعت مسبقا، وهو ما يعني أنه بالإمكان تجهيز آلة حاسوب بحيث تكون قادرة على إثبات كل النظريات الرياضية. لقد أجاب كورت غودل خلال الثلاثينات من القرن الماضي عن هذا السؤال بالنفي، مبرهنًا في نظريتين شهيرتين أن هناك قضايا رياضية لا يمكن البتّ فيها.

يمكن تقديم فكرة برهان غودل كالتالي:

السؤال: هل يمكن صنع آلة تقدم إجابات صائبة عن كل سؤال يطرح عليها؟

الجواب: لا.

لنوضّح ذلك: هب أن هذه الآلة موجودة. يقترح كورت غودل الجملة التالية: “هذه الآلة لن تقول أبدا بأن هذه الجملة صحيحة”. إذا رمزنا للآلة بالحرف ل وللجملة السابقة بالحرف ق استطعنا صياغتها كالتالي: ” ل لن تقول أبدا إن ق صحيحة”.

يطرح غودل بعد ذلك السؤال التالي على ل: هل ق صحيحة؟ ماذا ستجيب الآلة التي لا تخطئ أبدا:

* الحالة الأولى: إذا أجابت عن سؤال غودل بنعم فمعنى ذلك أن “ل لن تقول إن ق صحيحة” أي إن ق خاطئة، لكن الإجابة بنعم عن السؤال “هل ق صحيحة؟” تعني أيضا أن ق صحيحة. وهذا تناقض.

* الحالة الثانية: إذا أجابت عن سؤال غودل بالنفي فمعنى ذلك أن ل تقول إن ق صحيحة. لكن الإجابة بلا عن السؤال “هل ق صحيحة؟” تعني أيضا أن ق خاطئة. وهذا تناقض.

وهكذا، إذا افترضنا أن ل لا تقدم إلا أجوبة صحيحة ولا تخطئ أبدا فإنها لن تجيب عن السؤال المطروح ما دام جوابها سيؤدي في كل الأحوال إلى تناقض. وبما أنها لن تجيب عن سؤال غودل فهذا يعني أن ” ل لن تقول أبدا إن ق صحيحة”. وبالتالي فإن ق صحيحة!

ومن ثمّ نصل إلى النتيجة التالية: الإجابة عن سؤال غودل هي “نعم” والآلة ل صامتة وعاجزة عن البتّ فيها!

قضية اللانهاية

من الأمثلة الشائعة حول القضايا غير القابلة للبتّ قضية تتعلق باللانهاية. لنشرح ذلك بإيجاز: كان عالم الرياضيات الألماني الشهير جورج كنتور Cantor Georg (1845-1918) قد أبدع في نظرية المجموعات وحاول ترتيبها حسب عدد عناصرها: إذا كان عدد عناصر المجموعة منتهيا فلا مشكلة في هذا الترتيب، أما إذا كان غير منته فهو يطرح سؤالا عويصا لأن ذلك يتطلب ترتيب اللانهايات.

على سبيل المثال، دعنا نشر إلى مجموعات الأعداد الأربع التالية: مجموعة الأعداد الطبيعية (وهي 0، 1، 2، 3، 4،…)، ومجموعة الأعداد الصحيحة (وهي 0، 1، -1، 2، -2، 3، -3، 4، -4…)، ومجموعة الأعداد الناطقة أو الكسرية ( وهي كل الأعداد التي تكتب على شكل كسر عددين صحيحين)، ومجموعة الأعداد الحقيقية المؤلفة من الأعداد الناطقة السابقة الذكر ومن الأعداد الصماء (وهي جذور الأعداد التي لا تساوي أعدادا كسرية، وما شابهها…).

نلاحظ هنا أن عدد عناصر كل مجموعة من هذه المجموعات الأربع عدد غير منته. ومع ذلك يمكن البرهان على أن المجموعات الثلاث الأولى لها نفس عدد العناصر، وهي توصف بالمجموعات “العدودية”، بمعني أننا نستطيع “تعداد” عناصرها واحدا واحدا على الرغم من كثرتها! وهذا العدد يعتبره علماء الرياضيات “اللانهاية الأول” في ترتيب اللانهايات. أما المجموعة الرابعة (مجموعة الأعداد الحقيقية) فتمّ البرهان على أن عدد عناصرها يمثل “اللانهاية الثاني”، وهو أكبر من “اللانهاية الأول”!

لم يكن هناك مشكلة في إثبات ذلك عند كنتور بل المشكلة هي في السؤال التالي: هل هناك لانهاية محصور بين اللانهاية الأول واللانهاية الثاني؟! إن ما يُعرف في الرياضيات بـ”فرضية المستمر”  Continuum hypothesisالتي طرحها كنتور هي الفرضية القائلة “لا يوجد لانهاية محصور بين اللانهاية الأول واللانهاية الثاني” ! وأثبت عالم الرياضيات الأمريكي بول كوهين Paul Cohen (1934-2007) عام 1963 أن “فرضية المستمر” غير قابلة للبتّ!

عودة إلى مسارات الألعاب

انشغل علماء الرياضيات حديثا بقضية الألعاب المطاطية التي تحدثنا عنها في مطلع المقال وبمساراتها، وتساءلوا: هل كان بالإمكان تحديد مسار تلك الألعاب من نقطة البداية إلى النهاية؟ يبدو الأمر صعبًا. فعلماء المحيطات يعلمون أن تيارات المحيط الهادي من الأنظمة “الفوضوية” (أي الخارجة عن السيطرة) التي لا يمكن وصفها رياضيًا بدقة من خلال استخدام معادلات نافييه-ستوكس Navier-Stokes التي تصف حركة الموائع (أي السوائل والغازات). لماذا؟ لأن تلك المعادلات لا بد من مدّها بمعطيات أولية قبل أن نطلب منها مسار حركة كل لعبة أو كل الألعاب.

وقد بيّنت الدراسات الرياضية أن حلول تلك المعادلات بالغة الحساسية للظروف الأولية، لدرجة يستحيل معها عمليًا تحديد المكان الذي ستتجه إليه التيارات والمكان الذي ستحمل إليه كل لعبة من تلك الألعاب. لا بد أن نشير إلى أنه على الرغم من قدم وضع هذه المعادلات -التي يرجع تاريخها إلى النصف الأول من القرن التاسع عشر- فإن بعض جوانبها المطروحة هنا لاتزال غامضة. ولأهمية موضوعها خصص لها معهد كلاي Clay الأمريكي عام 2000 مكافأة بمليون دولار تُمنح لمن يجيب عن الأسئلة المطروحة بخصوصها وذلك ضمن “مسائل الألفية السبع”.

وفي هذا السياق، عكف فريق مكوّن من باحثين في الرياضيات يعملون في إسبانيا وفرنسا على دراسة هذا الموضع فبرهنوا خلال شهر مايو 2021، ضمن بحث نشر في مجلة تصدرها أكاديمية العلوم الأمريكية، على أن هذه القضية غير قابلة للبت، وهو ما يفسّر أن الكثير من الألعاب المطاطية لم يتم التعرف عن مكانها حتى الآن!! ذلك هو شأن العلم، يتقدم وتظهر نظريات له من حيث لا نتوقع!

توضح الخريطة بالخط الأحمر الأماكن التي وصلتها الألعاب خلال الفترة الممتدة من مطلع عام 1992 إلى 2007. أما السهم الأسود فيبيّن مكان انطلاق السفينة (هونغ كونغ) وموقع العاصفة التي أسقطت حاوية الألعاب في المحيط.