جسور مدينة كونيجسبيرغ: لغز أثمر ولادة فرع رياضياتي جديد
أثمر حل لغز الجسور السبعة لمدينة كونيجسبيرغ انبثاق فرع رياضياتي هو نظرية المخطط البياني Graph Theory، التي أصبحت موضوعاً غنياً بنتائج نظرية ولها تطبيقات عملية كثيرة

أحمد محمد جواد الحكيم
باحث وأكاديمي في علم الرياضيات
تتسم معظم الألغاز التي يتناقلها الناس عادة بالبساطة، وتسعى إلى تحقيق المتعة والتسلية والترفيه واختبار القدرات العقلية للفرد، من خلال التحدي والإثارة. لكن مع بساطة هذه الألغاز فقد استحوذ قسم منها على اهتمام بعض علماء الرياضيات، الذين احتاجوا من أجل حلها إلى نهج جديد من التفكير العقلي يعتمد كثيراً على الحدس وقوة التمثيل البياني لهذه الألغاز، بدلا من الطريقة الاستنتاجية المنطقية.
ومن الألغاز العملية القليلة جداً التي أدى حلها إلى فرع جديد في الرياضيات، هو لغز جسور مدينة كونيجسبيرغ Königsberg الروسية، الذي أجاب عن تساؤلاته عالم الرياضيات السويسري ليونارد أويلر Leonhard Euler (1707-1783م). وكان من ثمرات هذا الحل انبثاق فرع جديد في الرياضيات هو نظرية المخطط البياني Graph Theory، التي أصبحت موضوعاً غنياً بنتائج نظرية، ولها تطبيقات عملية عديدة، كتنظيم جدول المحاضرات لأساتذة الجامعة، أو تنظيم جداول زمنية للمصانع والمؤسسات الخدمية، أو إيجاد حلول مثلى لشبكات التوزيع والنقل.
بداية ظهور لغز الجسور
في القرن الثامن عشر الميلادي انبثقت فكرة إمكانية عبور جسور مدينة كونيجسبيرغ القديمة التي اعتاد سكانها المشي والتنزه في أرجائها، من خلال عبور نهر يقسمها قسمين، يدعى بريغل، باستخدام جميع الجسور المبنية فوقه وهي سبعة. وكانوا يسلّون أنفسهم بمسألة إيجاد مسار كامل يمر بكل أقسام المدينة، بشرط أن يجتازوا كل جسر مرة واحدة فقط. لكن بعد أن جرّبوا العديد من المسارات المختلفة لم يفلح أحد في إيجاد مسار يحقق الشرط الأساسي، فتحولت المسألة إلى لغز محيّر لا يعرفون جوابه.
ونشب جدال بين أهل المدنية حول حل هذا اللغز، فاعتقد بعضهم باستحالة إيجاد مسار كهذا، وساور آخرون الشك في ذلك. والذين تيقنوا أن ذلك مستحيل الحدوث لم يعرفوا سببه؛ هل هو نقص في قدراتهم العقلية أم أنه ناجمٌ من طبيعة المسألة. نعم هناك من اكتشف مساراً لكنه يمر بجسر أو أكثر مرتين. وانتشر خبر هذا اللغز في العديد من مناطق أوروبا، لكن السكان الذين لم يتوصلوا إلى إجابة محددة له طلبوا مساعدة العالم أويلر، الذي كان يعمل في أكاديمية العلوم بمدينة سان بطرسبرغ الروسية حينذاك، فأثبت استحالة الوصول إلى هذا المسار.
وهذا اللغز أو المسألة نجدها في مقالات ودراسات وكتب رياضياتية كثيرة. لكن هناك من غير أو أضاف توضيحات مفيدة إلى هذا اللغز، وبشكل أساسي قضية نقطة بدء المسار ونهايته، وما إذا كان المسار مستمراً أو منقطعاً. لأن العلاقة بين نقطة الانطلاق والانتهاء لم تكن مذكورة في النص الأصلي للغز، وفي مقالات عديدة في العصر الحالي. ومن الطبيعي أن يكون المسار مستمراً، غير منقطع، أي لا يُسمح بالقفز إلى الماء أو استعمال زورق أو غيره، هذا أولاً، ثانياً أن من الطبيعي أيضاً أن تكون نقطة الانطلاق والانتهاء هي نفسها، لأن البدء بجولة في أي مكان في المدينة يتعين الرجوع إلى مكان الانطلاق. وحتى لو افترضنا جدلاً أن نقطة الانطلاق تختلف عن نقطة الانتهاء، فإن ذلك لن يؤدي إلى إيجاد مسار يحقق الشرط الرئيسي وهو المرور بكل جسر مرة واحدة.
حل أويلر لمسألة الجسور
أدرك أويلر أن المسألة لا تتوافق مع السياق العام السائد في الرياضيات في ذلك الوقت، وأنها تتطلب نوعاً جديدا من التحليل، لذا ليس هناك حاجة للمسافات الدقيقة، وأن المعلومات النسبية، والخصائص المكانية هي كل ما يحتاج إليه. وفي العام ذاته، أي 1736م، اعتبر المسألة تابعة لهندسة المكان. وتوصل إلى قاعدة يمكن من خلالها معرفة ما إذا كان هناك حل أم لا لكل المسائل الشبيهة بها، ولأي عدد من الجسور وبأي ترتيب. وهذا الحل قدمه أويلر عام 1735م (أو 1736م) إلى أكاديمية العلوم في سان بطرسبرغ التي كان يعمل بها.
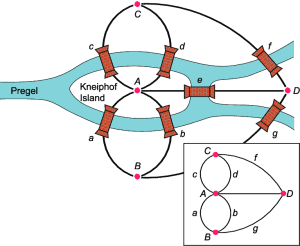
بدأ أويلر محاولته لحل لغز الجسور باتباع المسارات المحتملة الممكنة، لكنه رفضها لصعوبتها بسبب العدد الكبير من المسارات. لذلك تحوّل إلى الحل التحليلي، بعد أن استعان برسم الخريطة الطبيعية لمدينة كونيجسبيرغ، وهي مفرغة من أي أماكن أو شوارع أو بيوت أو أي شيء ليس له علاقة بهذه المسألة، وصاغها بالأحرف الأبجدية. فقد رمز لأقسام المدينة الأربعة بالحروف الكبيرة A،B،C،D، والجسور بالحروف الصغيرة a،b،c،d،e،f،g. ولاحظ أنه يمكن الإشارة إلى عبور أي جسر بزوج من الرموز، يشير الأول إلى الجزء الذي تتم مغادرته، والجزء الآخر هو الذي يتم الوصول إليه. ففي العبور من A إلى B، على سبيل المثال يدون الرمزان AB، ويجب أن يبدأ العبور التالي في السلسلة برمز B، ولو تم العبور من B إلى D لامتدت السلسلة هكذا: ABD (في مسار أويلر لا يهم أي جسر نسلكه). وكل جسر تالٍ يضيف رمزاً إلى السلسلة وهكذا. ومن الضروري ملاحظة أن عدد الحروف (الكبيرة) في الرحلة هو أكثر بواحد من عدد الجسور التي تم عبورها. لأن الرحلة AB تعبر جسراً واحداً، والرحلة ABD تعبر جسرين وهكذا.
ولكي تتحقق شروط المسألة (وهي عبور كل جسر مرة واحدة فقط، والبدء والانتهاء من النقطة نفسها) فقد بيّن أويلر، أن مدينة كونيجسبيرغ لها سبعة جسور. وهذا يعني أننا بحاجة إلى ثمانية أحرف لرحلة تتكون من سبعة جسور، تبدأ وتنتهي بالرمز نفسه. وبما أنه توجد خمسة جسور تصل المنطقة A بالأجزاء الأخرى، فإن من السهل ملاحظة ورود رمز A ثلاث مرات في السلسلة لو أُريد عبور هذه الجسور الخمسة في الحل ذي الثمانية أحرف الذي نبحث عنه. وكذلك فإن لكل منطقة من المناطق B،C،D ثلاثة جسور تؤدي إليها، لذلك فإن كلا منها بحاجة إلى أن يظهر مرتين. لكن مجموع ثلاث واثنين واثنين واثنين هو تسع (عدد المناطق التي يجب المرور بها) وليس ثمانيا (نلاحظ أنه يمكن المرور بأي منطقة أكثر من مرة)، وبما أننا يجب أن نمر بثماني مناطق لسبعة جسور (حسب الاستنتاج في البداية) فهذا يعني أننا لا نستطيع السير خلال المدينة باستعمال كل جسر مرة واحدة بالضبط، وأنه يستحيل وجود مسار يحقق الشروط المطلوبة.
قاعدة عامة لأعداد الجسور
لم يتوقف أويلر عند إثبات استحالة إيجاد مسار لمسألة جسور مدينة كونيجسبيرغ السبعة، إنما واصل البحث لإيجاد قاعدة عامة تبين ما إذا كان المسار ممكناً أو لا، في مدن أخرى، تحوي أي عدد من الجسور والمناطق، وبيّن الشروط الضرورية والكافية للسير بحيث يمكن عبور كل جسر مرة واحدة والمرور على كل مناطق المدينة، وهي:
– إذا كان هناك أكثر من منطقتين يتصل بكل منهما عدد فردي من الجسور، فإن المسار غير ممكن. من هذه القاعدة يمكن أن نستنتج استحالة إيجاد مسار لمسألة جسور كونيجسبيرغ السبعة؛ لأن فيها أربع مناطق لكل منها عدد فردي من الجسور.
– إذا كان هناك منطقتان فقط لكل منهما عدد فردي من الجسور، فإن المسار ممكن دائماً إذا بدأ من إحدى هاتين المنطقتين وانتهى بالأخرى. لكن ينبغي أن نلاحظ قضيتين: الأولى، إذا كانت هناك منطقة واحدة فقط عدد جسورها فردي، فإن المسار غير ممكن. الثانية، في حالة وجود منطقتين فرديتين فإنه لا يمكن البدء والانتهاء بالمنطقة ذاتها.
– إذا لم تكن هناك أي منطقة لها عدد فردي من الجسور، بمعنى أن جميع المناطق لها عدد زوجي من الجسور، فالمسار المطلوب ممكن من أي منطقة، بمعنى أن المسار يمكن أن يبدأ وينتهي في المنطقة ذاتها.
أهمية بداية المسارونهايته
ومن الأهمية بمكان أن نبيّن أنه عند تحقق شروط إيجاد مسار يمر بكل الجسور مرة واحدة فقط، فإن بداية المسار ونهايته لهما أهمية بالغة في حالة الواقع العملي، لأن المُتَنَزِه عندما ينطلق من نقطة معينة، أي من منطقته، فإنه يجب أن يعود إلى النقطة ذاتها. لكن في الحل المجرد، في الرياضيات، فإن تطابق أو عدم تطابق نقطة البداية والنهاية ليس ذا أهمية. القضية الثانية أن أويلر بيّن أنه إذا تحققت تلك الشروط في الحل العام، أي شروط الضرورة، فإن المسار ممكن، وطرح أسبابا حدسية استكشافية عن سبب كونها صحيحة، لكنه لم يبرهن على شروط الكفاية.
واستنتج أويلر القواعد السابقة حينما لاحظ الشرط الأساسي، وهو عبور كل جسر مرة واحدة، بمعنى أن كل منطقة يجب أن تحوي عددا زوجيا من الجسور متصلا بها. لأنه حينما يدخل المُتَنَزِه إحدى المناطق بواسطة جسر معين، عند ذاك يجب عليه أن يغادرها بواسطة جسر آخر. لذلك فإن أي منطقة تحتاج إلى جسرين إذا دخلها مرة واحدة، وإلى أربعة جسور إذا دخلها مرتين، وهكذا، ما عدا منطقتي انطلاق المسار وانتهائه، يمكن أن تحوي عددا فرديا من الجسور إذا لم تكونا متطابقتين. وبما أن أي مسار يمكن أن يبدأ وينتهي بمنطقتين على الأكثر، فإن ذلك يوجب أن تكون هناك على الأكثر منطقتين فرديتين.
إن عبقرية أويلر لا تكمن فقط في إجابته القاطعة باستحالة إيجاد مسار في المدينة يحقق الشروط المطلوبة، إنما بابتكاره نهجاً جديداً في التفكير والتحليل استنتج به هذه الإجابة، وأدى في النهاية إلى ولادة فرع جديد في الرياضيات هو “نظرية المخططات البيانية”.
شكل (1)
شكل (2)